LEARNING QUADRATIC
RELATIONS
Learning At Home
“Enrichment beyond the classroom”
EXPAND AND SIMPLIFY

To expand is to get rid of the brackets.
Distributive law:
a(b + c) = ab + ac
We use the distributive law to write expressions such as 3(x + 1) in a form that has no brackets,
3(x + 1) = 3 x x + 3 x 1
= 3x + 3
1. Expand 2xy (4y - 2x)
=8xy^2 - 4x^2y
Why?
2xy multiples everything in the bracket, including the variables
2. 2(3x-5)-7(3x-4)
=(6x-10)-(21x-28)
=6x-21x=-15x
=-10-(-28)=18
-15x-18
3. 3(4x-10)+3(3x+4)
=(12x-30)+(9x+12)
=21x-18
LEARN TO FACTOR
WHAT DOES IT MEAN TO FACTOR?
-A number or quantity that when multiplied with another produces a given number or expression.
For example;
Factor the number 6. When you are being asked to factor, you are really being asked; What numbers were multiplied to make 6?
COMMON FACTORING
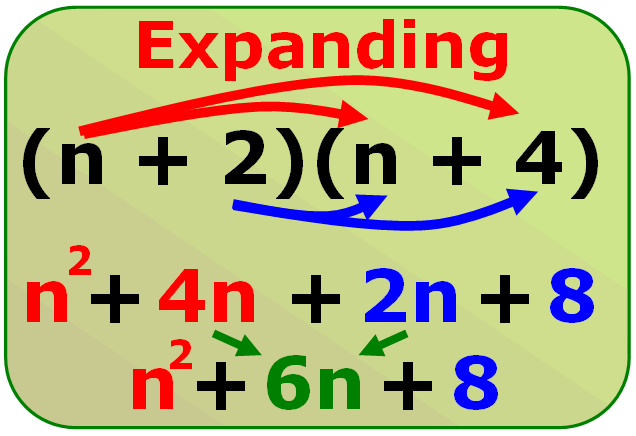
You know how to multiply two brackets together. (expand and simplify)
(a + b)(c + d) = ac + ad + bc + bd
If you have the expression on the right hand side how can you change it back to the two brackets on the left hand side?
When you common factor, you are breaking it up by finding a number or expression/exponant that is common
Example: (2x+6)
there is a common factor of 2
=2(x+2)
Example 2:


Factoring Simple Trinomials x^2+bx+c
Factor:
Example 1:
1) g^2+11g+30
=(g+5)(g+6)
Factor:
Example 2:
2)n^2+8n+7
=(n+1)(n+7)
Factor:
Example 3:
3) r^2-3r+2
=(r-2)(r-5)
=(r-1)(r-2)
Factoring Complex Trinomials ax^2+bx+c
You know what a simple trinomial is,
But what is a complex trinomial?
How do you factor it?
A complex trinomial is a trinomial that does NOT start with 1.
For example: 3x^2+18x+12
2x^2+11x+15
Step 1: look for a common factor, and factor it into 2 sections
Break into 2 factors; guess and check
=(2x+5)(x+3)
you need to find 2 numbers that multiply to 15.
6x^2+11x+3
=(3x+1)(2x+3)
=6x^2+9x+2x+3 check your work.
=6x^2+11x+3
Factor perfect square trinomials and a difference of squares
Things you should know:
Perfect squares start with a squared number and end with a squared number with a number in between (a^2+2ab+b^2)
Difference of squares have nothing in the middle. (a^2+b^2)

Example 1:
e^2-20e+100
=(e+10)^2
Example 2:
u^2-18u+81
=(u-9)^2
Example 3:
r^2-8r+16
=(r-4)^2